Deep neural networks offer a lot of value to statisticians, particularly in increasing accuracy of a machine learning model. The deep net component of a ML model is really what got A.I. from generating cat images to creating art—a photo styled with a van Gogh effect:

So, let’s take a look at deep neural networks, including their evolution and the pros and cons.
What is a deep neural network?
At its simplest, a neural network with some level of complexity, usually at least two layers, qualifies as a deep neural network (DNN), or deep net for short. Deep nets process data in complex ways by employing sophisticated math modeling.
To truly understand deep neural networks, however, it’s best to see it as an evolution. A few items had to be built before deep nets existed.
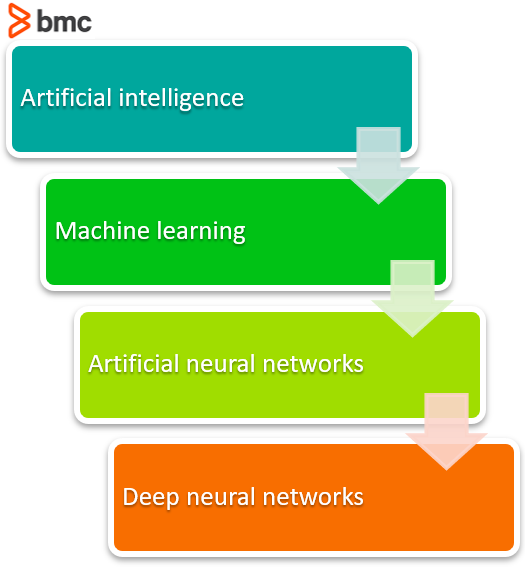
The evolution to Deep Neural Networks (DNN)
First, machine learning had to get developed. ML is a framework to automate (through algorithms) statistical models, like a linear regression model, to get better at making predictions. A model is a single model that makes predictions about something. Those predictions are made with some accuracy. A model that learns—machine learning—takes all its bad predictions and tweaks the weights inside the model to create a model that makes fewer mistakes.
The learning portion of creating models spawned the development of artificial neural networks. ANNs utilize the hidden layer as a place to store and evaluate how significant one of the inputs is to the output. The hidden layer stores information regarding the input’s importance, and it also makes associations between the importance of combinations of inputs.
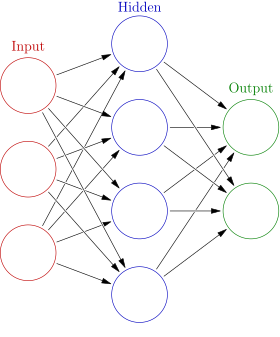
One hidden layer is considered an Artificial Neural Network (ANN)
Deep neural nets, then, capitalize on the ANN component. They say, if that works so well at improving a model—because each node in the hidden layer makes both associations and grades importance of the input to determining the output—then why not stack more and more of these upon each other and benefit even more from the hidden layer?
So, the deep net has multiple hidden layers. ‘Deep’ refers to a model’s layers being multiple layers deep.
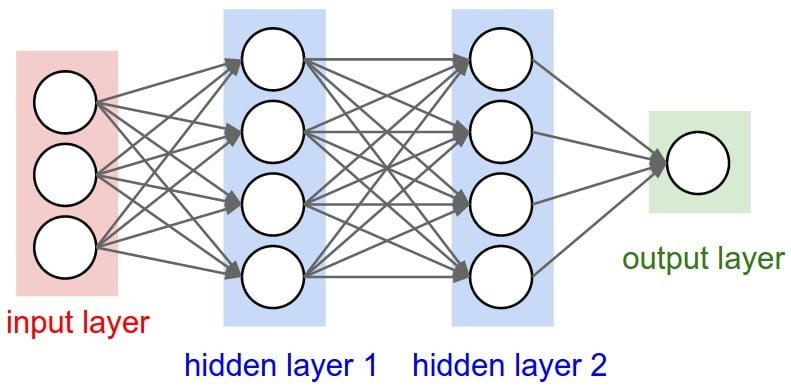
Two or more hidden layers comprise a Deep Neural Network
Improving accuracy: The black box problem
Deep nets allow a model’s performance to increase in accuracy. They allow a model to take a set of inputs and give an output. The use of a deep net is as simple as copying and pasting a line of code for each layer. It doesn’t matter which ML platform you use; directing the model to use two or 2,000 nodes in each layer is as simple as typing the characters 2 or 2000.
But using these deep nets creates a problem: How do these models make their decisions? When utilizing these simple tools, a model’s explainability is reduced significantly.
The Deep Net allows a model to make generalizations on its own and then store those generalizations in a hidden layer, the black box. The black box is hard to investigate. Even if the values in the black box are known, they don’t exist within a framework for understanding.
The problem of explainability
A teacher might be able to say that 10% of the grade is participation, 20% is homework, 30% is quizzes, and 40% is tests. These numbers are both known and can be easily understood to predict the overall score. That means a teacher’s rubric is an explainable model. It needs to be explainable for a student to know how to get a good grade in the class.
Another example: a simple machine learning model could take data collected from a simple high school physics class and calculate the equation for gravity—or the force of gravity experienced at the Earth’s surface.
| Ball Weight | Drop Height | Fall Time |
|---|---|---|
| 500 g | 10m | 1.5s |
| 400 g | 7m | 1s |
| … | … | … |
A normal statistical, linear regression model can be used to give the equation that predicts the results. If the inputs Ball Weight and Drop Height are used to predict how long the fall time will be, then the model can be used to create an equation that lets us predict the result every time.
- We learn the equation is: x (m) = 1/2 • g (m/s^2) • t^2 (s^2)
- We learn that the object’s mass is totally unnecessary to predicting the result.
When the hidden layer is introduced, the model will still be able to return the correct result for a falling ball. But now, the equation that can inform which input contributes to the total output cannot be determined. The model is unexplainable.
The problem of explainability continues to be explored and progress is being made. Deep nets provide great value to a model’s performance, but the cost of using them is an inability to explain exactly how the model gets to the answer it does. (By the way, the secret to life is 42.)
Additional resources
For more on this topic, explore our BMC Machine Learning & Big Data Blog and these articles:
- Machine Learning: Hype vs Reality
- How Machine Learning Benefits Businesses
- The Role of Machine Learning in Datacenter Network Security
- Bias and Variance in Machine Learning
- Using TensorFlow to Create a Neural Network (with Examples), part of our Machine Learning Guide
- Apache Spark Guide, with articles and step-by-step tutorials







