A business imperative for companies of all sizes, cloud computing allows organizations to consume IT services on a usage-based subscription model. The promise of cloud computing depends on two viral metrics, service reliability and availability, to evaluate the dependability of a system. Vendors offer service level agreements (SLAs) to meet specific standards of reliability and availability. An SLA breach not only incurs cost penalty to the vendor but also compromises end-user experience of apps and solutions running on the cloud network.
Though reliability and availability are often used interchangeably, they are different concepts in the engineering domain. Let’s explore the distinction between reliability and availability, then move into how both are calculated.
What is reliability?
Reliability is the probability that a system performs correctly during a specific time duration. During this correct operation, no repair is required or performed, and the system adequately follows the defined performance specifications.
Reliability follows an exponential failure law, which means that it reduces as the time duration considered for reliability calculations elapses. In other words, reliability of a system will be high at its initial state of operation and gradually reduce to its lowest magnitude over time.
What is availability?
Availability refers to the probability that a system performs correctly at a specific time instance (not duration). Interruptions may occur before or after the time instance for which the system’s availability is calculated. The service must be operational and adequately satisfy the defined specifications at the time of its usage.
Availability is measured at its steady state, accounting for potential downtime incidents that can (and will) render a service unavailable during its projected usage duration. For example, a 99.999% (Five-9’s) availability refers to 5 minutes and 15 seconds of downtime per year.
Incident and service metrics
Before discussing how reliability and availability are calculated, an understanding of incident service metrics used in these calculations is required. These metrics are computed through extensive experimentation, experience, or industrial standards; they are not observed directly. Therefore, the resulting calculations only provide relatively accurate understanding of system reliability and availability.
The graphic, below, and following sections outline the most relevant incident and service metrics:
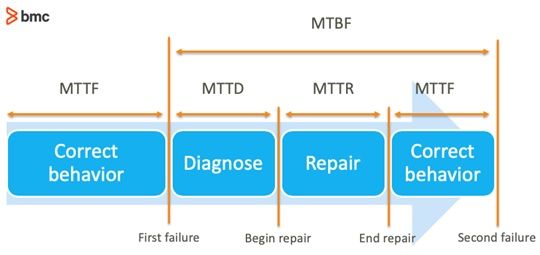
Failure rate
The frequency of component failure per unit time. It is usually denoted by the Greek letter λ (Lambda) and is used to calculate the metrics specified later in this post. In reliability engineering calculations, failure rate is considered as forecasted failure intensity given that the component is fully operational in its initial condition. The formula is given for repairable and non-repairable systems respectively as follows:
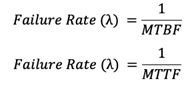
Repair rate
The frequency of successful repair operations performed on a failed component per unit time. It is usually denoted by the Greek letter μ (Mu) and is used to calculate the metrics specified later in this post. Repair rate is defined mathematically as follows:
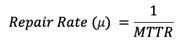
Mean time to failure (MTTF)
The average time duration before a non-repairable system component fails. The following formula calculates MTTF:

Mean time between failure (MTBF)
The average time duration between inherent failures of a repairable system component. The following formulae are used to calculate MTBF:

Mean time to recovery (MTTR)
The average time duration to fix a failed component and return to operational state. This metric includes the time spent during the alert and diagnostic process before repair activities are initiated. (The average time solely spent on the repair process is called mean time to repair.)

Mean time to detection (MTTD)
The average time elapsed between the occurrence of a component failure and its detection.
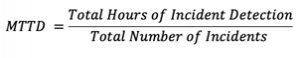
Reliability and availability calculations
The calculations below are computed for reliability and availability attributes of an individual component. The failure rate can be used interchangeably with MTTF and MTBF as per calculations described earlier.
- Reliability is calculated as an exponentially decaying probability function which depends on the failure rate. Since failure rate may not remain constant over the operational lifecycle of a component, the average time-based quantities such as MTTF or MTBF can also be used to calculate Reliability. The mathematical function is specified as:
- Availability determines the instantaneous performance of a component at any given time based on time duration between its failure and recovery. Availability is calculated using the following formula:
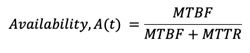
Calculation of multi-component systems
IT systems contain multiple components connected as a complex architectural. The effective reliability and availability of the system depends on the specifications of individual components, network configurations, and redundancy models. The configuration can be series, parallel, or a hybrid of series and parallel connections between system components. Redundancy models can account for failures of internal system components and therefore change the effective system reliability and availability performance.
A reliability block diagram (RBD) may be used to demonstrate the interconnection between individual components. Alternatively, analytical methods can also be used to perform these calculations for large scale and complex networks. RBD demonstrating a hybrid mix of series and parallel connections between system components is provided:
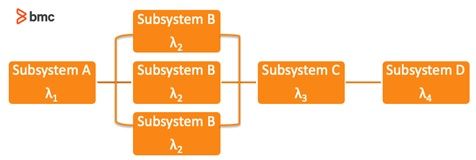
The basics of an RBD methodology are highlighted below.
Using failure rates
The effective failure rates are used to compute reliability and availability of the system using these formulae:
- For series connected components, the effective failure rate is determined as the sum of failure rates of each component.
- For N series-connected components:
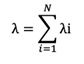
- For parallel connected components, MTTF is determined as the reciprocal sum of failure rates of each system component.
- For N parallel-connected components:
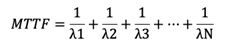
- For hybrid systems, the connections may be reduced to series or parallel configurations first.
Using availability and reliability specifications
Calculate reliability and availability of each component individually.
- For series connected components, compute the product of all component values.
- For N series-connected components.

- For parallel connected components, use the formula:
- For N parallel-connected components.
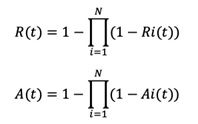
- For hybrid connected components, reduce the calculations to series or parallel configurations first.
It can be observed that the reliability and availability of a series-connected network of components is lower than the specifications of individual components. For example, two components with 99% availability connect in series to yield 98.01% availability. The converse is true for parallel combination model. If one component has 99% availability specifications, then two components combine in parallel to yield 99.99% availability; and four components in parallel connection yield 99.9999% availability. Adding redundant components to the network further increases the reliability and availability performance.
It’s important to note a few caveats regarding these incident metrics and the associated reliability and availability calculations.
- These metrics may be perceived in relative terms. Failure may be defined differently for the same components in different applications, use cases, and organizations.
- The value of metrics such as MTTF, MTTR, MTBF, and MTTD are averages observed in experimentation under controlled or specific environments. These measurements may not hold consistently in real-world applications.
Organizations should therefore map system reliability and availability calculations to business value and end-user experience. Decisions may require strategic trade-offs with cost, performance and, security, and decision makers will need to ask questions beyond the system dependability metrics and specifications followed by IT departments.
Additional resources
The following literature is referred for system reliability and availability calculations described in this article:







